Dominio y Rango de una función cuadrática o de segundo grado

Summary

El video ofrece un curso sobre cómo identificar y trabajar con funciones cuadráticas, dividido en tres partes. Primero, se enseña a reconocer una función cuadrática por su forma y exponentes. En segundo lugar, se muestran gráficas de funciones cuadráticas para entender sus características. Por último, se explica cómo determinar el dominio y el rango de estas funciones, destacando la importancia del vértice para entender su comportamiento. El video también incluye un ejercicio práctico para que los estudiantes puedan aplicar lo aprendido.

Takeaways

• 📚 El curso trata sobre cómo encontrar el dominio y el rango de una función cuadrática.
• 🔍 Para identificar una función cuadrática, es necesario que la variable independiente 'x' esté al cuadrado y no haya exponentes mayores.
• 🚫 Las funciones que incluyen términos con exponentes mayores que dos o que tienen 'x' en el denominador no son cuadráticas.
• 📉 El dominio de cualquier función cuadrática es todos los números reales, ya que la parábola se extiende desde menos infinito hasta infinito horizontalmente.
• 📈 El rango de una función cuadrática se determina por la orientación de la parábola; si abre hacia arriba, el rango comienza desde el vértice hasta infinito, y si abre hacia abajo, comienza en menos infinito hasta el vértice.
• 📌 El vértice de la parábola es un punto crucial que indica el inicio del rango y representa el punto más bajo o alto de la función, dependiendo de su orientación.
• 📐 La gráfica de la función cuadrática es una parábola, y su forma (abertura hacia arriba o hacia abajo) es determinada por el signo del coeficiente 'a' de la término 'x al cuadrado'.
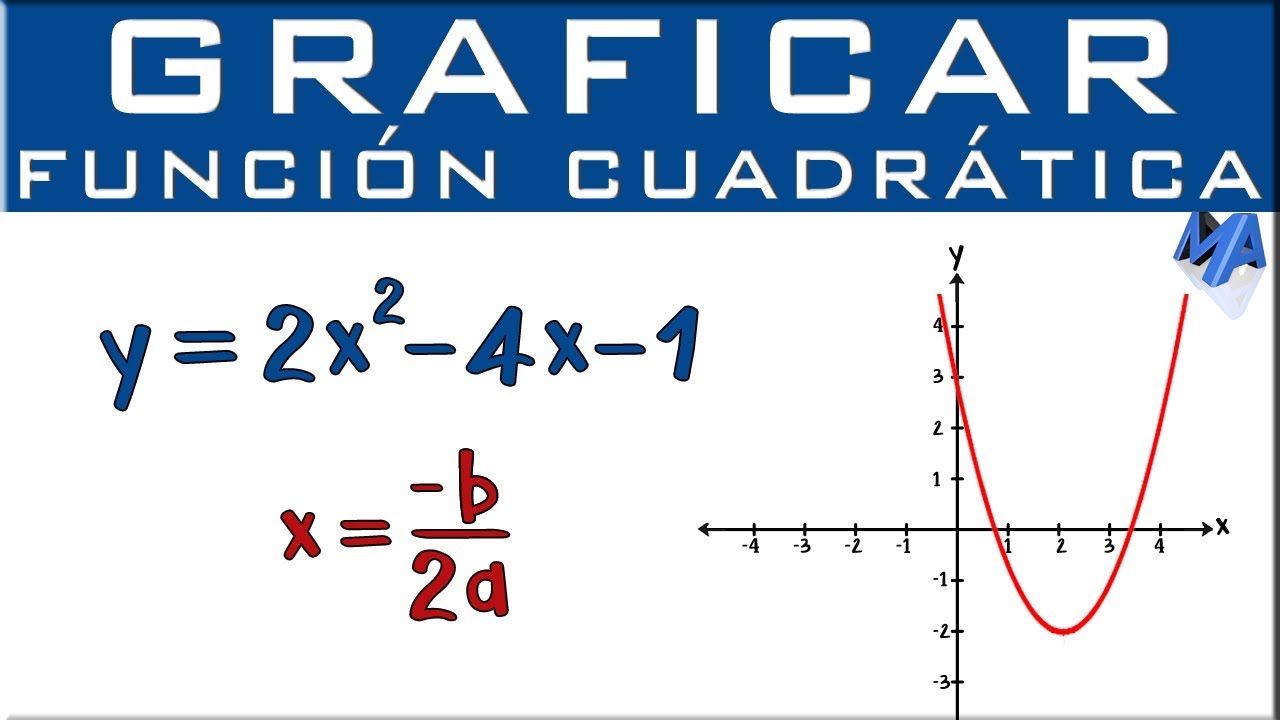
• 🔢 El coeficiente 'a' junto con 'b' y 'c' son claves para encontrar el vértice de la parábola, utilizando la fórmula -b/(2a) para encontrar la coordenada x del vértice.
• 📝 Al sustituir el valor de x del vértice en la función, se puede encontrar la coordenada y del vértice, que es necesaria para determinar el rango.
• 📚 El script ofrece un ejercicio práctico para que los estudiantes puedan aplicar los conceptos aprendidos sobre cómo encontrar el vértice y determinar el dominio y el rango de una función cuadrática.

Q & A

¿Qué es un dominio en matemáticas y cómo se relaciona con una función cuadrática?

El dominio de una función es el conjunto de todos los valores posibles de la variable independiente, en este caso 'x', para los cuales la función es definida. Para una función cuadrática, el dominio es siempre todos los números reales, ya que las funciones cuadráticas son definidas para cualquier valor de 'x'.

¿Cómo se define el rango de una función cuadrática?

El rango de una función cuadrática es el conjunto de todos los valores que puede tomar la función, es decir, los valores de 'y'. Depende de la dirección en la que se abre la parábola (hacia arriba o hacia abajo) y se determina a partir del vértice de la parábola.

¿Cómo se reconoce una función cuadrática?

Una función cuadrática se reconoce por tener un término de 'x' al cuadrado como el término de mayor grado, y no tener 'x' con un exponente mayor que dos. Además, 'x' no debe estar en el denominador de la función.

¿Por qué es importante reconocer si una función es cuadrática antes de encontrar su dominio y rango?

Es importante reconocer si una función es cuadrática porque el proceso para encontrar el dominio y rango es específico para este tipo de funciones. Si la función no es cuadrática, se deben utilizar métodos diferentes para determinar su dominio y rango.

¿Qué es el vértice de una parábola y cómo se relaciona con el rango de una función cuadrática?

El vértice de una parábola es el punto en el que la parábola cambia de dirección, es decir, el punto más bajo si la parábola se abre hacia arriba o el punto más alto si la parábola se abre hacia abajo. El vértice es crucial para determinar el rango de una función cuadrática, ya que marca el inicio o el final del rango, dependiendo de la dirección de la parábola.

¿Cómo se encuentra el vértice de una parábola cuadrática?

El vértice de una parábola cuadrática se encuentra utilizando la fórmula x = -b/(2a), donde 'a' es el coeficiente del término 'x' al cuadrado y 'b' es el coeficiente del término en 'x'. Una vez que se conoce la coordenada x del vértice, se puede sustituir en la función para encontrar la coordenada y.

¿Cómo se determina si una parábola se abre hacia arriba o hacia abajo?

Una parábola se abre hacia arriba si el coeficiente 'a' del término 'x' al cuadrado es positivo, y se abre hacia abajo si 'a' es negativo.

¿Cuál es la fórmula para encontrar la coordenada x del vértice de una parábola cuadrática y cómo se aplica?

La fórmula para encontrar la coordenada x del vértice es x = -b/(2a). Se aplica sustituyendo los valores de 'a' y 'b' de la función cuadrática en la fórmula para calcular la x del vértice.

¿Cómo se relaciona el valor de 'a' en una función cuadrática con la forma de la gráfica de la función?

El valor de 'a' en una función cuadrática determina la dirección en la que se abre la parábola. Si 'a' es positivo, la parábola se abre hacia arriba, y si 'a' es negativo, la parábola se abre hacia abajo. Además, el valor absoluto de 'a' también afecta la estrechez de la parábola.

¿Por qué el dominio de todas las funciones cuadráticas es todos los números reales?

El dominio de todas las funciones cuadráticas es todos los números reales porque las funciones cuadráticas no tienen restricciones en los valores que puede tomar la variable independiente 'x'. No hay valores de 'x' que muestren comportamientos indefinidos o que no se puedan calcular.