La elipse (método de los 4 centros)
Summary
TLDREn este video, se presenta el método de los 'cuatro centros' para trazar una elipse, explicando paso a paso cómo determinar los puntos clave en los ejes mayor y menor. Con una longitud de 13 unidades para el eje mayor y 9 para el eje menor, se detallan las técnicas de marcar puntos, trazar diagonales y usar un compás para generar los arcos necesarios. A lo largo del proceso, el instructor también hace énfasis en la importancia de la fe en Cristo, destacando la condición matemática de que el eje menor debe ser igual o mayor a dos tercios del eje mayor para aplicar el método correctamente.
Takeaways
- 😀 Se inicia la lección con un saludo fraterno y un mensaje de esperanza a través de Cristo Jesús.
- ✏️ Se presenta un nuevo método para trazar una elipse, conocido como el 'método de los cuatro centros.'
- 📏 Se establecen dos ejes, el mayor y el menor, con longitudes específicas: 13 cm y 9 cm, respectivamente.
- 🔄 Los ejes deben ser perpendiculares entre sí y se deben trazar desde un punto central.
- 📍 Se determinan puntos en el eje menor y en el eje mayor utilizando la diferencia entre los dos ejes.
- 📐 El método implica trazar diagonales entre los puntos establecidos en los ejes.
- 🔍 Se utiliza un compás para trazar arcos que intersecten con las diagonales, formando la elipse.
- ⚖️ Es importante que la longitud del eje menor sea igual o mayor a dos tercios de la longitud del eje mayor para aplicar este método.
- 📝 Se realiza un chequeo para confirmar que las proporciones se cumplen con las medidas elegidas.
- 💡 El mensaje final refuerza que sólo en Cristo Jesús hay salvación y esperanza para el mundo.
Q & A
¿Cuál es el tema principal del video?
-El tema principal es cómo trazar una elipse utilizando el método de los cuatro centros.
¿Qué mensaje espiritual se comparte al inicio del video?
-Se comparte un mensaje sobre la gracia y salvación en Cristo Jesús, animando a los espectadores a confiar sus vidas a Él.
¿Cuáles son las longitudes asignadas para los ejes mayor y menor?
-El eje menor se establece en 9 centímetros y el eje mayor en 13 centímetros.
¿Cómo se determina el centro de la elipse?
-El centro de la elipse se marca en 6.5 centímetros, que es la mitad de la longitud del eje mayor.
¿Qué pasos se siguen para identificar los puntos en el eje menor?
-Se determina la diferencia entre el eje mayor y el eje menor (4 unidades) y se marcan dos puntos, 4 unidades por encima y por debajo del origen.
¿Cómo se calculan los puntos en el eje mayor?
-Los puntos en el eje mayor se establecen como tres cuartos de la diferencia entre los ejes mayor y menor.
¿Por qué es importante prolongar las diagonales en el proceso?
-Prolongar las diagonales ayuda a intersectar correctamente los arcos que se trazan para formar la elipse.
¿Qué papel tiene el compás en la construcción de la elipse?
-El compás se utiliza para trazar arcos desde puntos clave, facilitando la creación de la forma de la elipse.
¿Qué condición debe cumplir el eje menor para aplicar este método?
-La longitud del eje menor debe ser igual o mayor a dos tercios de la longitud del eje mayor.
¿Qué se concluye sobre la relación entre la geometría y la fe en el video?
-El video concluye que la verdadera salvación y esperanza se encuentran solo en Cristo Jesús, resaltando la conexión entre la fe y el aprendizaje.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

Trazado de una elipse: Método de los círculos concéntricos
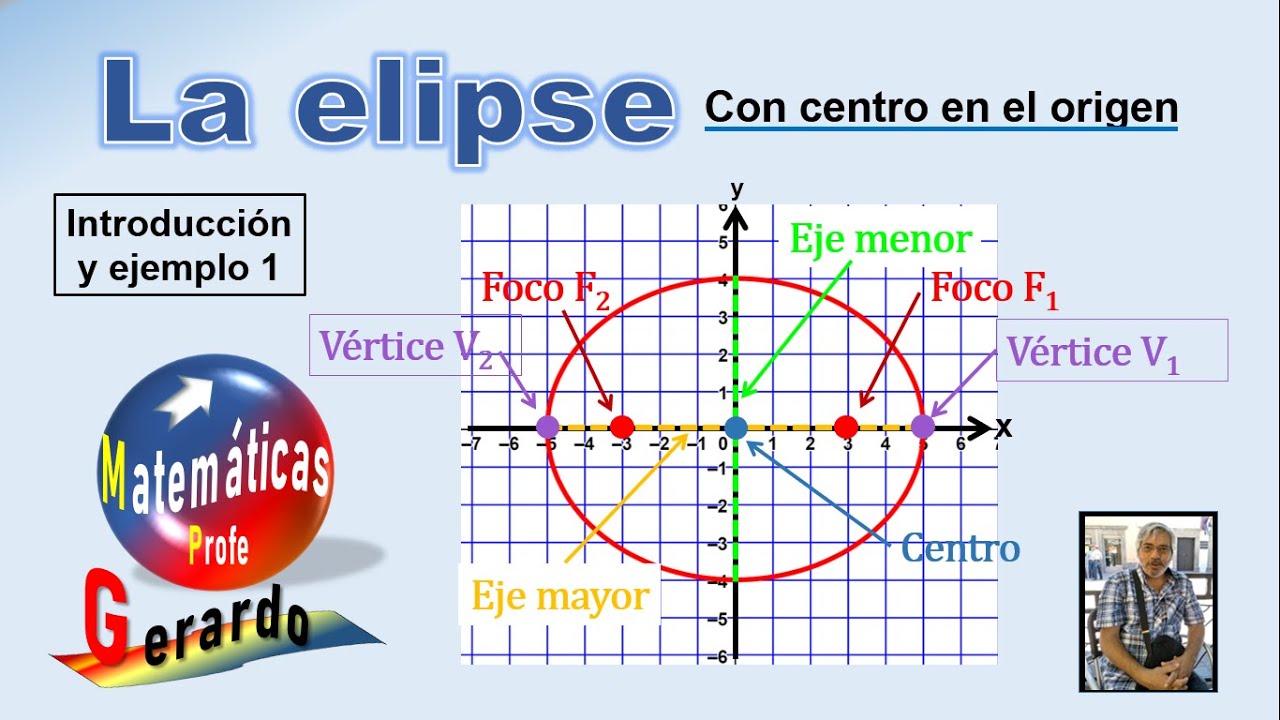
La elipse con centro en el origen. Introducción y ejemplo 1.

✅ELIPSE con centro FUERA del ORIGEN [100% 𝙀𝙛𝙚𝙘𝙩𝙞𝙫𝙤 😎🫵💯] Geometría Analítica

Ecuación canónica de la Elipse | Centro en (h,k)
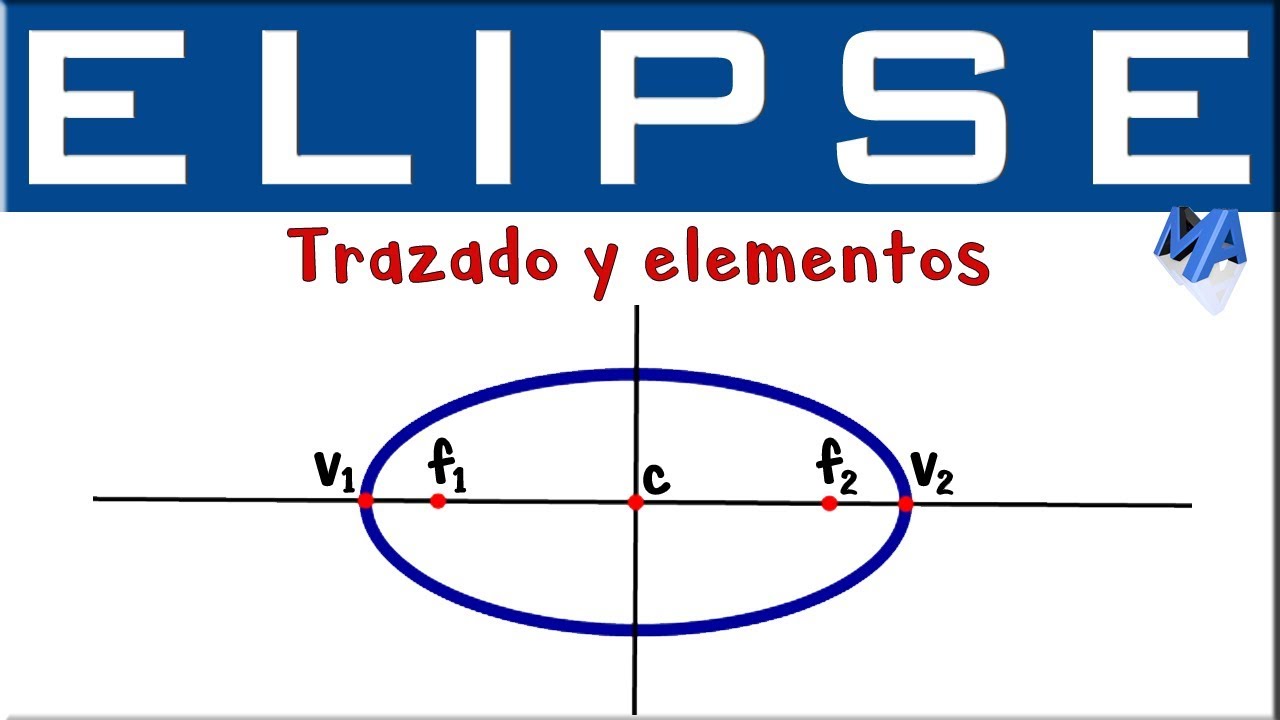
Elipse trazado y elementos | Introducción

🏉 ELIPSE: Concepto y elementos (focos, vértices, Eje Mayor, Eje Menor, L.R.) | Juliana la profe
5.0 / 5 (0 votes)
