78. GEOMETRÍA ANALÍTICA: COORDENADAS POLARES
Summary
TLDREn este video, se explora el sistema de coordenadas polares y su conversión al sistema cartesiano y viceversa. El presentador explica cómo en ciertos contextos, como la navegación, es más útil usar un ángulo y una distancia en lugar de coordenadas rectangulares. Se abordan las fórmulas clave para transformar coordenadas entre ambos sistemas y se ofrecen ejemplos prácticos para ilustrar el proceso. También se destaca la importancia de comprender los ángulos en diferentes cuadrantes y el uso correcto de calculadoras para realizar estos cálculos. El video concluye invitando a los espectadores a hacer preguntas si tienen dudas.
Takeaways
- 📍 Las coordenadas polares se utilizan para encontrar puntos en un plano con una distancia y un ángulo en lugar de coordenadas cartesianas (X, Y).
- 🧭 Este sistema es útil en aplicaciones como la navegación de aviones y barcos, ya que permite ubicar un punto basado en la distancia y el ángulo.
- 🎯 El punto de referencia en el sistema polar se llama 'polo' y reemplaza al origen en el sistema cartesiano.
- 🔄 El ángulo en coordenadas polares se mide en grados, en sentido contrario a las manecillas del reloj para ángulos positivos y en sentido horario para ángulos negativos.
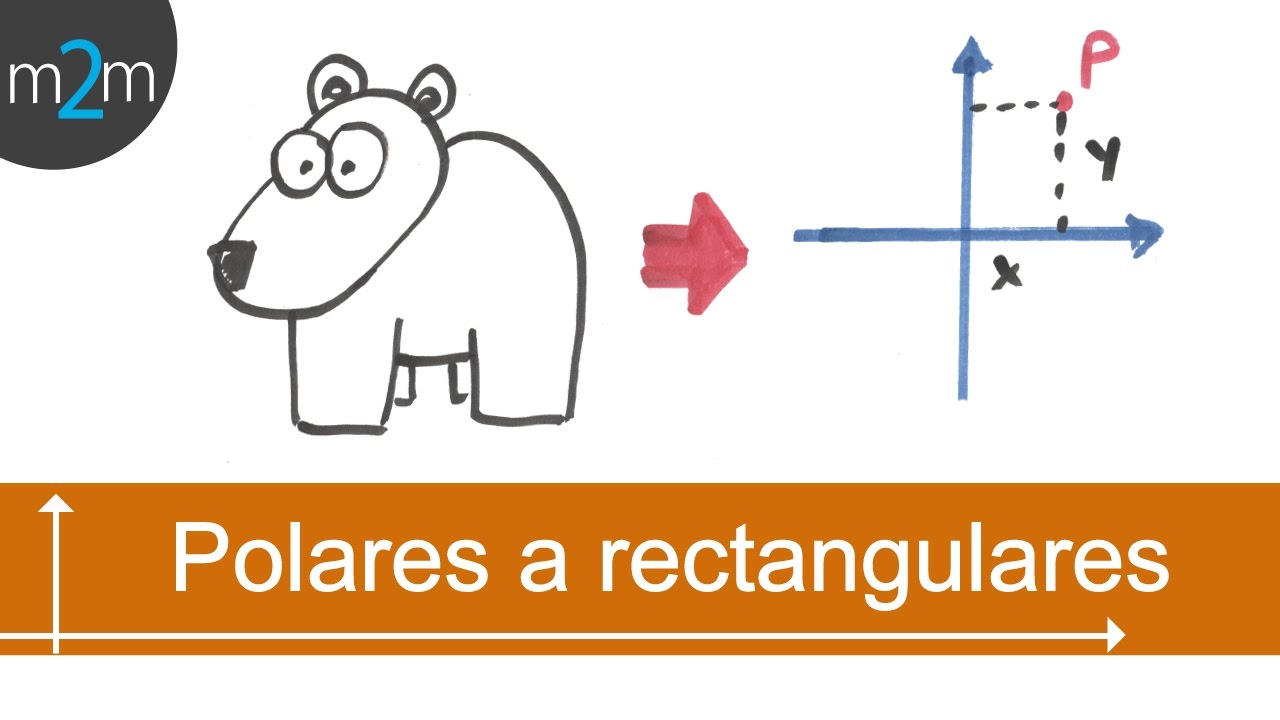
- 📐 Las fórmulas clave para convertir de polar a cartesiano son: X = r * cos(θ) y Y = r * sin(θ), donde r es la distancia y θ el ángulo.
- 💡 Para convertir de coordenadas cartesianas a polares, se utiliza la tangente inversa para obtener el ángulo (θ = arctan(Y/X)) y el teorema de Pitágoras para calcular la distancia (r = √(X² + Y²)).
- ⚠️ En algunos cuadrantes, se debe ajustar el ángulo calculado sumando o restando 180° o 360° dependiendo del caso.
- 📊 En el tercer cuadrante, se debe sumar 180° al ángulo obtenido con la tangente inversa para obtener la dirección correcta.
- 📏 La calculadora científica debe estar configurada en grados para realizar las conversiones correctamente.
- 📝 Las fórmulas clave a recordar son X = r * cos(θ), Y = r * sin(θ), θ = arctan(Y/X) y r = √(X² + Y²) para hacer conversiones entre sistemas polares y cartesianas.
Q & A
¿Qué es el sistema de coordenadas polares?
-El sistema de coordenadas polares es un método para definir la posición de un punto en un plano bidimensional mediante una distancia y un ángulo en lugar de las coordenadas cartesianas x e y.
¿Cuál es la diferencia entre las coordenadas cartesianas y polares?
-Las coordenadas cartesianas utilizan dos valores, x e y, para definir la posición de un punto en un plano. En cambio, las coordenadas polares usan una distancia desde el origen (radio) y un ángulo (theta) para definir la misma posición.
¿Cómo se determina el ángulo en el sistema polar?
-El ángulo en el sistema polar se determina por la dirección desde el eje polar (similar al eje x cartesiano) hacia el punto de interés, usualmente medido en sentido contrario a las manecillas del reloj.
¿Qué sucede si quiero definir un ángulo en sentido de las manecillas del reloj?
-Si se desea definir un ángulo en sentido de las manecillas del reloj, el ángulo se representa como negativo.
¿Cómo se pasa de coordenadas polares a cartesianas?
-Para pasar de coordenadas polares a cartesianas, se utilizan las fórmulas x = r * cos(theta) y y = r * sen(theta), donde r es la distancia y theta el ángulo.
¿Cuál es la fórmula para convertir x cartesiano a polar?
-La fórmula para encontrar el ángulo en coordenadas polares es theta = arctan(y/x), y para el radio se usa r = sqrt(x^2 + y^2).
¿Cómo se ajusta el ángulo cuando se trabaja en diferentes cuadrantes del plano cartesiano?
-Cuando se trabaja en cuadrantes distintos del primero, el ángulo obtenido mediante la función arctan(y/x) debe ajustarse sumando o restando multiples de 180 grados para reflejar la posición correcta en el sistema polar.
¿Qué significa un radio negativo en coordenadas polares?
-Un radio negativo en coordenadas polares indica que la distancia se mide en la dirección opuesta al ángulo theta, es decir, se extiende en la dirección opuesta a la indicada por el ángulo desde el origen.
¿Por qué es importante recordar que la calculadora siempre da el ángulo entre la línea y el eje x?
-Es importante recordar esto porque la calculadora proporciona el ángulo en relación con el eje x, pero en el sistema polar, el ángulo se mide entre el eje polar y la línea que une el origen con el punto, lo que puede estar en un cuadrante diferente y requiere ajustes para obtener el ángulo correcto.
¿Cómo se determina si el ángulo en coordenadas polares es positivo o negativo?
-El ángulo en coordenadas polares es positivo si la dirección desde el origen hacia el punto es en sentido contrario a las manecillas del reloj, y negativo si es en el sentido de las manecillas del reloj.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

Transformar Coordenadas Cartesianas en Coordenadas Polares y viceversa

Convertir coordenadas cartesianas (rectangulares) a polares |👇👇video actualizado en la descripción👇👇

Convertir coordenadas rectangulares a polares

COORDENADAS CARTESINAS, ESFERICAS Y CILINDRICAS

Plano polar y coordenadas polares.
Convertir coordenadas polares a rectangulares (cartesianas)
5.0 / 5 (0 votes)
