How to Solve Quadratic Equations by Completing the Square? Grade 9 Math
Summary
TLDRIn this educational video, the teacher guides viewers through solving quadratic equations using the method of completing the square. Starting with the equation x^2 + 6x - 2 = 0, the tutorial demonstrates transposing constants, adding a term to form a perfect square trinomial, and then expressing it as a square of a binomial. The process concludes with extracting square roots to find the values of x, resulting in x = ±√11 - 3. The video promises a follow-up on handling equations with coefficients greater than one, encouraging viewers to stay tuned.
Takeaways
- 📚 The video discusses solving quadratic equations by completing the square, an alternative to factoring and extracting square roots.
- 🔗 Links to previous videos on factoring and square root extraction are promised in the description box for continuity.
- 📉 The example equation given is x^2 + 6x - 2 = 0, which is challenging to factor, hence the focus on completing the square.
- ➡️ The first step in completing the square is to transpose the constant term to the other side of the equation, resulting in x^2 + 6x = 2.
- 🔢 To form a perfect square trinomial, calculate the value of b/2, square it, and add it to both sides of the equation, leading to x^2 + 6x + 9 = 11.
- 🟣 The expression is then rewritten as a square of a binomial, (x + 3)^2 = 11.
- 📐 Extracting the square roots gives x + 3 = ±√11, introducing the concept of both positive and negative solutions.
- 🔄 Isolating the variable x involves moving the +3 to the other side, resulting in x = -3 ± √11.
- 📝 The solutions to the equation are x1 = √11 - 3 and x2 = -√11 - 3, demonstrating the use of both positive and negative square roots.
- 🎥 The video concludes with a teaser for another video that will cover cases where the coefficient of the first term is greater than one.
Q & A
What is the main topic discussed in the video?
-The main topic discussed in the video is solving quadratic equations by completing the square.
Why is completing the square a useful method for solving quadratic equations?
-Completing the square is useful when the quadratic equation is difficult to factor, as it provides an alternative method to find the solutions.
What is the first step in completing the square for a quadratic equation with a leading coefficient of 1?
-The first step is to transpose the constant term to the other side of the equation, changing its sign in the process.
How do you determine the third term to make the expression a perfect square trinomial?
-You take the coefficient of the linear term (b), divide it by 2, and then square the result to get the third term.
What is the purpose of expressing the perfect square trinomial as a square of a binomial?
-Expressing it as a square of a binomial simplifies the equation and allows for the extraction of square roots to solve for x.
How do you isolate the variable x when completing the square?
-You isolate x by removing the linear term (if present) from the equation and transposing it to the other side.
What is the significance of the number 11 in the video's example?
-In the example, 11 is the sum of the constant term and the square of the number obtained from the linear term's coefficient divided by 2.
Why is it necessary to consider both the positive and negative square roots when solving for x?
-Considering both the positive and negative square roots ensures that all possible solutions for x are found, as square roots can have both positive and negative values.
How many solutions does the quadratic equation presented in the video have?
-The quadratic equation presented in the video has two solutions, x₁ and x₂.
What is the final form of the solutions for x in the example given in the video?
-The final form of the solutions for x are x = √11 - 3 and x = -√11 - 3.
What is the advice given for viewers who are new to the channel?
-The advice for new viewers is to like, subscribe, and hit the bell button to stay updated with the latest uploads.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

SOLVING QUADRATIC EQUATIONS USING QUADRATIC FORMULA | Grade 9 Learning Task 3 Week 1

How to Solve Quadratic Equations by Extracting the Square Root? @MathTeacherGon

Persamaan Kuadrat • Part 4: Menyelesaikan Persamaan Kuadrat dengan Rumus abc
Solving Quadratic Equations by Extracting the Square Roots by @MathTeacherGon

2. Ecuaciones cuadráticas completas, solución por el Método de completar el binomio
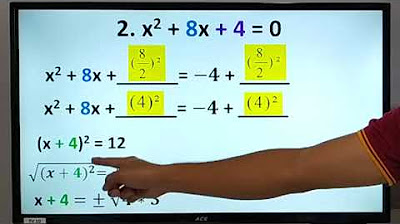
Math8 1G LV4 - Completing the Square and Quadratic Formula
5.0 / 5 (0 votes)
