GeoGebra Triángulo de Napoleón
Summary
TLDREn este tutorial, se muestra cómo construir el triángulo de Napoleon a partir de un triángulo equilátero utilizando el programa de diseño. Se explica cómo trazar lados y puntos usando comandos, emplear el compás para dibujar círculos y triángulos equiláteros, y encontrar intersecciones para formar el triángulo deseado. Se incluyen pasos para medir áreas y cambiar propiedades como color y grosor de línea para diferenciar los triángulos. El objetivo es aprender a utilizar herramientas del programa para resolver problemas geométricos de forma efectiva.
Takeaways
- 📐 El tutorial enseña cómo construir el triángulo de Napoleón a partir de un triángulo equilátero.
- 📍 Se inicia trazando lados y un punto nuevo utilizando un comando específico.
- 📏 Se utilizan coordenadas de segmentos para ubicar el punto de apoyo en la vista algebraica.
- 🔍 El compás es una herramienta clave para trazar círculos y radios, como se muestra en el proceso.
- 📉 Se muestra cómo utilizar el zoom para visualizar mejor los círculos y objetos en el programa.
- 🔄 Se eliminan cónicas intermedias para simplificar la visualización del triángulo equilátero.
- 🎯 Se selecciona el radio y se ubica el centro para trazar los triángulos equiláteros exteriores.
- 📌 Se utiliza la intersección de objetos para colocar puntos clave en la construcción del triángulo.
- 📐 Se construye el triángulo de Napoleón mediante la intersección de triángulos equiláteros y secciones.
- 🖍 Se personalizan los triángulos ajustando colores y estilos de línea para diferenciarlos.
- 📏 Se calcula el área del triángulo de Napoleón y se compara con el área del triángulo original.
Q & A
¿Qué es el triángulo de Napoleón y cómo se construye?
-El triángulo de Napoleón es una figura geométrica que se construye a partir de un triángulo equilátero. Se realiza trazando los puntos medios de los lados del triángulo equilátero y luego uniendo estos puntos con líneas para formar un nuevo triángulo equilátero más pequeño en su interior.
¿Qué herramienta se utiliza para trazar círculos en el programa mencionado en el tutorial?
-Se utiliza el compás para trazar círculos en el programa. Se selecciona el radio deseado y se coloca el centro en un punto específico para obtener el círculo.
¿Cómo se determina la intersección de los círculos en el tutorial?
-Para determinar la intersección de los círculos, se usan las herramientas del programa que permiten encontrar donde dos objetos se cruzan. Se selecciona la opción de intersección y se colocan los puntos correspondientes para obtener la intersección.
¿Cuál es el radio de la circunferencia utilizada para construir los triángulos equiláteros en el tutorial?
-El radio de la circunferencia utilizada para construir los triángulos equiláteros es de 10 unidades.
¿Cómo se eliminan los objetos innecesarios como las cónicas en el programa después de haberlos utilizado?
-Para eliminar los objetos innecesarios como las cónicas, se seleccionan y se borran del dibujo, dejando así el espacio más limpio y enfocado en los objetos relevantes.
¿Qué es el polígono y cómo se utiliza en el proceso de construcción del triángulo de Napoleón?
-El polígono es una herramienta que permite dibujar formas con múltiples lados. En el caso del triángulo de Napoleón, se utiliza para unir los puntos de intersección y formar el triángulo equilátero correspondiente.
¿Cómo se encuentran los puntos medios de los lados del triángulo equilátero en el programa?
-Se utiliza el comando que permite localizar el punto medio de cada línea. Se coloca el extremo del segmento y el programa automáticamente determina el punto medio.
¿Qué se hace después de trazar los segmentos entre los puntos medios para formar el triángulo de Napoleón?
-Después de trazar los segmentos entre los puntos medios, se unen estos puntos utilizando el polígono para formar el triángulo de Napoleón final.
¿Cómo se cambian las propiedades de un objeto, como el color y el grosor de las líneas, en el programa?
-Se selecciona el objeto con el botón derecho del mouse, se accede a las propiedades del objeto y se cambian los atributos deseados, como el color y el estilo de la línea.
¿Cómo se calcula el área del triángulo de Napoleón y del triángulo original en el programa?
-Para calcular el área, se selecciona el triángulo (verde para el de Napoleón y rojo para el original) y se utiliza la herramienta de área en el programa. Se asegura de seleccionar correctamente el triángulo para obtener el área correspondiente.
¿Qué se debe hacer para obtener el área del triángulo de Napoleón una vez calculada la del triángulo en apoyo?
-Para obtener el área del triángulo de Napoleón, se debe restar el área del triángulo en apoyo (interior) de la del triángulo total (exterior), utilizando las herramientas del programa para realizar esta operación.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Teorema de Napoleón
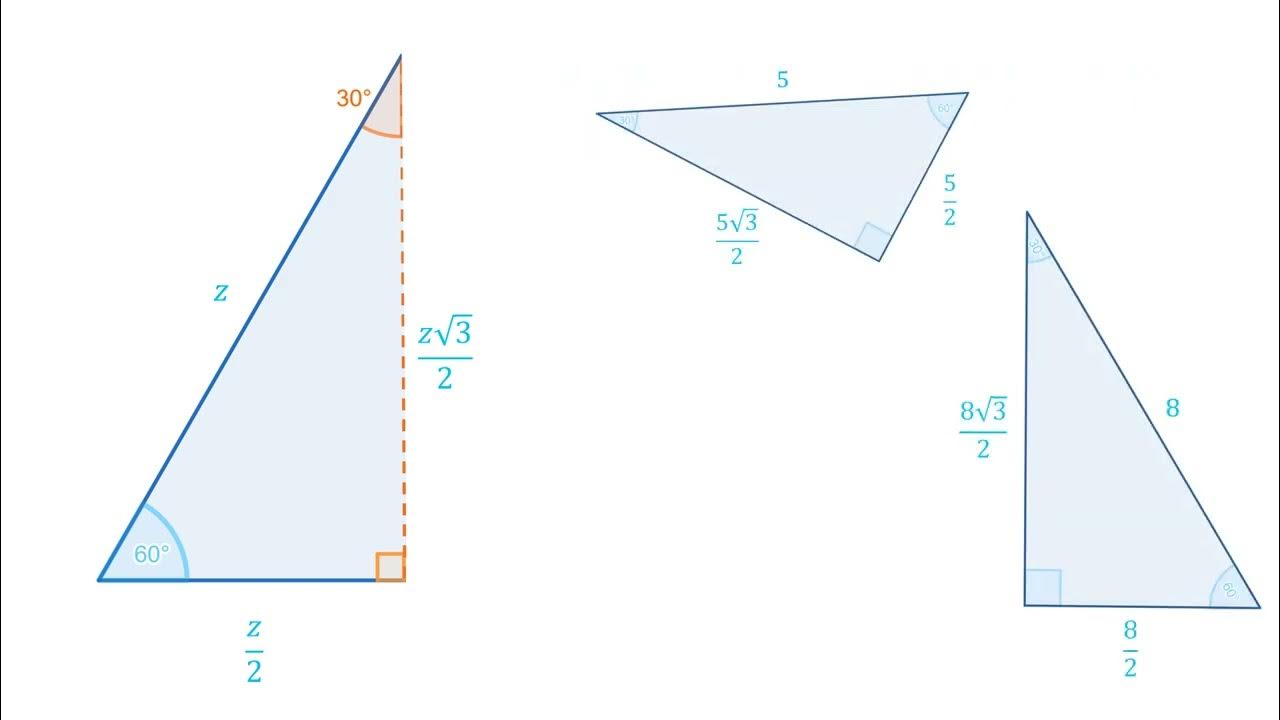
Razones Trigonométricas en Triángulos Especiales

🔺 TRIÁNGULO dados dos LADOS y el ÁNGULO común 📐 Dibujo técnico paso a paso

12. Programación en C - Operadores - Ejercicio Hipotenusa de un triángulo rectángulo

COMO CREAR un ALGORITMO para calcular el área de un triángulo y programar en PSeInt.

Polígonos regulares en GeoGebra. Gonzalo Vaca
5.0 / 5 (0 votes)
