TRANSFORMACIONES ISOMETRICAS Semana31 8°

Summary

En este video, se aborda el tema de las transformaciones isométricas, enfocándose en la traslación y la rotación de triángulos en un plano cartesiano. Se explica cómo mover un triángulo mediante traslaciones, modificando las coordenadas de sus vértices, y cómo rotarlo 180 grados alrededor del origen, invirtiendo sus posiciones. A través de ejemplos prácticos y gráficos, se ilustra cómo estas transformaciones no alteran el tamaño ni la forma del triángulo, sino solo su ubicación. El objetivo es que los estudiantes comprendan y apliquen estas transformaciones en problemas geométricos.

Takeaways

• 😀 Los transformaciones isométricas no cambian el tamaño ni la forma de una figura, solo su posición.
• 😀 La **traslación** mueve un objeto en el plano cartesiano, ajustando sus coordenadas por un valor específico en los ejes X e Y.
• 😀 Al realizar una traslación, cada vértice de un triángulo se ajusta según los desplazamientos dados en los ejes X e Y.
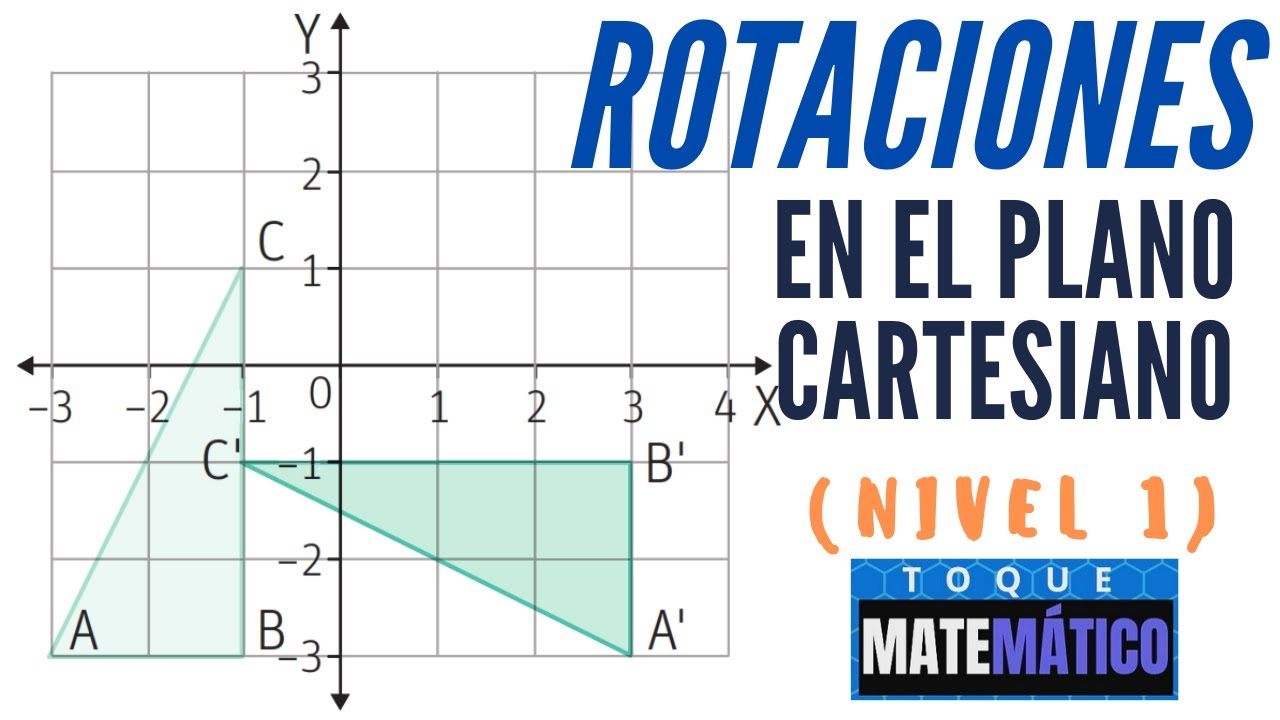
• 😀 Para realizar una **rotación de 180°** alrededor del origen, las nuevas coordenadas de cada vértice se obtienen negando las coordenadas originales.
• 😀 En una rotación de 180° alrededor del origen, las coordenadas de A (1,2) se convierten en (-1,-2), las de B (3,5) en (-3,-5) y las de C (5,2) en (-5,-2).
• 😀 El proceso de graficar implica primero colocar los puntos originales y luego conectar los vértices para formar un triángulo.
• 😀 El triángulo resultante de la rotación de 180° estará completamente invertido, con todas las coordenadas en la parte negativa del plano cartesiano.
• 😀 La reflexión también se mencionó como una transformación isométrica, pero no se profundizó en detalles.
• 😀 El tamaño y la forma de la figura no se alteran en una rotación o traslación, solo su orientación o posición en el plano.
• 😀 Es importante comprender cómo trasladar y rotar figuras para resolver ejercicios y aplicar estas técnicas en actividades académicas.

Q & A

¿Qué son las transformaciones isométricas?

Las transformaciones isométricas son aquellas que cambian la posición de una figura en el plano sin alterar su forma o tamaño. Ejemplos comunes de estas transformaciones son la traslación, la rotación y la reflexión.

¿Qué se entiende por traslación en el contexto de las transformaciones isométricas?

La traslación es una transformación en la que cada punto de una figura se mueve de manera uniforme en una dirección específica. En otras palabras, se mueve a lo largo de un vector definido, cambiando su posición sin cambiar su forma.

¿Cómo se realiza una traslación en un plano cartesiano?

Para realizar una traslación, se suman las cantidades correspondientes al eje x y al eje y a las coordenadas originales de cada vértice de la figura. Por ejemplo, mover un triángulo con un desplazamiento de +2 en x y -3 en y cambiará las coordenadas de cada vértice de acuerdo con estos valores.

¿Qué sucede con las coordenadas de un triángulo cuando se realiza una traslación?

Las coordenadas de cada vértice del triángulo se modifican sumando o restando un valor determinado a las coordenadas x y/o y, dependiendo de la dirección y magnitud del desplazamiento.

¿Qué implica la rotación de una figura 180 grados alrededor del origen?

Rotar una figura 180 grados alrededor del origen significa invertir tanto las coordenadas x como y de cada vértice de la figura. Esto transforma un punto (x, y) en (-x, -y), lo que genera una figura invertida respecto a la original.

¿Cómo se realiza una rotación de 180 grados de un triángulo con vértices A (1, 2), B (3, 5) y C (5, 2)?

Para rotar estos puntos 180 grados alrededor del origen, simplemente se cambian los signos de las coordenadas. El punto A (1, 2) se convierte en A' (-1, -2), B (3, 5) en B' (-3, -5), y C (5, 2) en C' (-5, -2).

¿Qué es una reflexión en las transformaciones isométricas?

La reflexión es una transformación que invierte la posición de una figura a través de una línea de reflexión, generando una imagen simétrica de la figura original.

¿Qué se conserva en una transformación isométrica?

En una transformación isométrica, la figura mantiene su forma y tamaño, lo que significa que no cambia ni la longitud de los lados ni los ángulos. Solo cambia la posición de la figura en el espacio.

¿Qué se debe hacer para graficar una figura después de realizar una traslación o rotación?

Para graficar una figura después de una traslación o rotación, se deben colocar las nuevas coordenadas de los vértices en el plano cartesiano y luego conectar los puntos para visualizar la nueva forma. Por ejemplo, tras realizar una rotación de 180 grados, la figura resultante debe estar invertida respecto a la original.

¿Cómo se determina la nueva posición de los vértices en una traslación o rotación?

La nueva posición de los vértices en una traslación se determina sumando o restando valores a las coordenadas x y y. En una rotación de 180 grados, se invierten los signos de las coordenadas x e y de cada vértice.