✔👍👉TUBO VENTURI. CÁLCULO de la VELOCIDAD con BERNOULLI, CONTINUIDAD y PASCAL [💪ENTRA y APRENDE!!!]
Summary
TLDREl guión ofrece una asesoría educativa sobre el cálculo de la velocidad del agua en un tubo de Venturi, utilizando la ecuación de Bernoulli y la ecuación de continuidad. Se describe un experimento con un líquido de densidad 5.5 veces mayor que la del agua, y se resuelve el problema de determinar la velocidad en una sección del tubo, donde se observa una diferencia de altura en los vasos comunicantes. El análisis concluye con la aplicación del principio de Pascal para calcular la diferencia de presiones y, finalmente, se determina la velocidad en la sección más ancha del tubo.
Takeaways
- 🌀 El video trata sobre el cálculo de la velocidad del agua en un tubo de Venturi utilizando la mecánica de fluidos.
- 📐 Se presenta un problema de dos tubos con secciones diferentes, uno 10 veces más grande que el otro, y un líquido de densidad 5.5 veces mayor que el agua.
- 📉 La altura del líquido en el vaso central es dos centímetros por encima del de la derecha y cinco por encima del de la izquierda, indicando diferencias de presión.
- 💧 La ecuación de Bernoulli se utiliza para relacionar la presión, la energía cinética y la energía potencial en los dos puntos del tubo.
- 🔄 La ecuación de continuidad afirma que el caudal (flujo volumétrico) es constante a través de las secciones del tubo.
- ⏱ La velocidad en la sección más estrecha del tubo (sección 2) es 10 veces mayor que en la más ancha (sección 1).
- 📚 Se necesita conocer la densidad del agua y la diferencia de presiones entre las secciones para calcular la velocidad en la sección 1.
- 📉 El principio de Pascal se aplica en los vasos comunicantes para determinar la relación de presiones entre diferentes puntos del sistema.
- 📏 Se utiliza la ecuación de hidrostática para calcular la presión en puntos específicos del sistema, basándose en la altura y densidad del fluido.
- ⚖️ La densidad del fluido marrón es 5.5 veces la densidad del agua, lo que influye en el cálculo de la presión y la velocidad del fluido.
- 🔢 Al final, se calcula la diferencia de presiones y se utiliza para determinar la velocidad del agua en la sección 1, obteniendo un valor aproximado de 0.1635 metros por segundo.
Q & A
¿Qué es el ejercicio de mecánica de fluidos tratado en el script?
-El ejercicio trata sobre el cálculo de la velocidad del agua en un tubo de Venturi, donde hay una transición de una sección de tubo a otra más estrecha, y se utiliza la ecuación de Bernoulli y la ecuación de continuidad para resolverlo.
¿Cuál es la relación entre las secciones de los tubos mencionados en el script?
-La sección del segundo tubo es diez veces menor que la del primer tubo.
¿Qué fluido se utiliza en el ejercicio y cuál es su densidad en relación con la del agua?
-Se utiliza un líquido cuya densidad es 5.5 veces mayor que la del agua.
¿Cómo se relaciona la altura del líquido en los vasos comunicantes con la velocidad en la sección del tubo?
-La diferencia de altura del líquido en los vasos comunicantes indica la diferencia de presión que se utiliza para calcular la velocidad del agua en la sección del tubo.
¿Cuál es la ecuación utilizada para relacionar la velocidad en las dos secciones del tubo?
-La ecuación de continuidad se utiliza para relacionar la velocidad en las dos secciones del tubo, indicando que el caudal en ambas secciones es igual.
¿Por qué la velocidad es mayor en la sección más estrecha del tubo?
-La velocidad es mayor en la sección más estrecha debido a que el flujo debe pasar por una sección más pequeña, lo que reduce la área y, según la ecuación de continuidad, aumenta la velocidad.
¿Cómo se utiliza la ecuación de Bernoulli para calcular la velocidad en la sección del tubo de mayor área?
-La ecuación de Bernoulli se utiliza para establecer una relación entre la presión, la energía cinética y la energía potencial en ambas secciones del tubo. Al simplificar la ecuación, dado que las alturas son iguales, se puede resolver para encontrar la velocidad en la sección del tubo de mayor área.
¿Cómo se calcula la diferencia de presión entre las dos secciones del tubo?
-La diferencia de presión se calcula utilizando el principio de Pascal y las alturas del líquido en los vasos comunicantes, considerando la densidad del agua y del fluido.
¿Cuál es el resultado aproximado de la velocidad del agua en la sección del tubo de mayor área?
-El resultado aproximado de la velocidad del agua en la sección del tubo de mayor área es de 0.1635 metros por segundo.
¿Cómo se relaciona la densidad del fluido con la densidad del agua en el script?
-La densidad del fluido es 5.5 veces la densidad del agua, lo que se utiliza para calcular la diferencia de presión y, en consecuencia, la velocidad del agua en la sección del tubo.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Tubo de Venturi caseiro e equação de Bernoulli.

MECÁNICA DE FLUIDOS.ECUACIÓN BERNOULLI, SE USA:¿LA PRESIÓN MANOMÉTRICA O ABSOLUTA?[ENTRA Y ENTÉRATE]
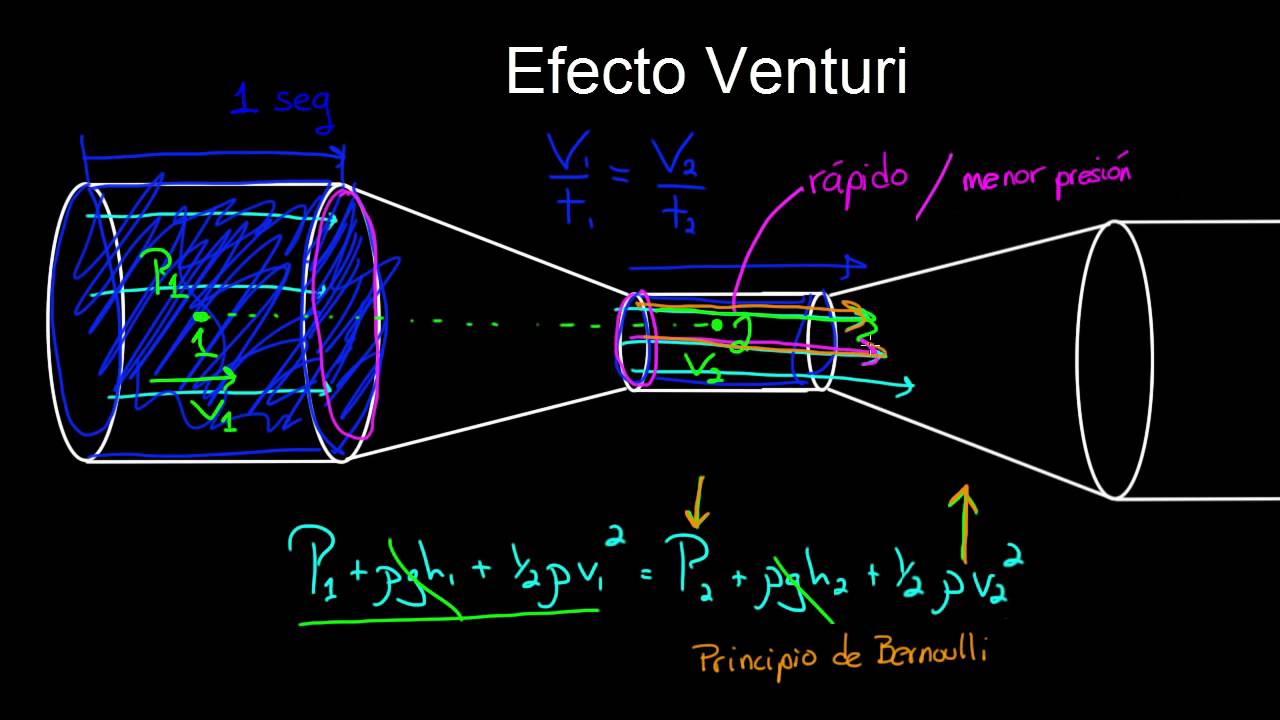
Efecto Venturi y tubos Pitot | Fluidos | Física | Khan Academy en Español

Aplicaciones de la ecuación de Bernoulli

EFECTO VENTURI: ¡Cómo un Tubo Puede Controlar la Presión y la Velocidad del Aire!

Fluidos (parte 12)
5.0 / 5 (0 votes)
