Práctica04 Ejercicio1
Summary
TLDREn este ejercicio, se exploran matrices para determinar si sus columnas son linealmente independientes, generadoras o bases del espacio \( \mathbb{K}^n \). A través de la reducción de matrices, se analizan diferentes casos, evaluando la independencia lineal y la generación de vectores. Se explican conceptos clave como pivotes y filas de ceros, así como la extracción de bases a partir de matrices iniciales. El ejercicio también aborda cómo ampliar bases usando la matriz identidad y calcula los pivotes necesarios para encontrar soluciones. Cada caso se discute con ejemplos específicos para ilustrar los resultados.
Takeaways
- 📋 El ejercicio consiste en analizar una serie de matrices para determinar si sus columnas son linealmente independientes, generadoras o bases de un espacio.
- 📊 Se utiliza el entorno de SageMath para trabajar con matrices y realizar reducciones por filas, lo que facilita la identificación de características como independencia lineal y generación.
- 🧮 El objetivo es reducir las matrices para ver si cumplen con las condiciones de independencia lineal y si pueden generar el espacio completo.
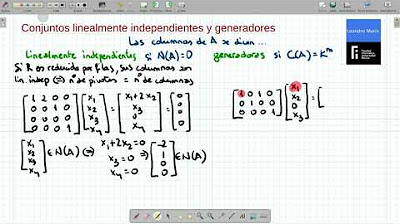
- 📌 Si todas las columnas de una matriz son pivotes y no hay filas de ceros, entonces las columnas son generadoras y linealmente independientes, por lo tanto, constituyen una base del espacio.
- 🚫 Si una matriz tiene filas de ceros o no todas sus columnas son pivotes, no son generadoras ni linealmente independientes.
- 🔄 Para algunos casos se debe extraer una base de la matriz original a partir de las columnas que sean linealmente independientes, identificadas en la matriz reducida.
- 📝 En el caso de vectores linealmente independientes, se sugiere ampliarlos a una base utilizando vectores de la matriz identidad, observando qué vectores son necesarios.
- 📈 En matrices donde algunas columnas no son pivotes o hay filas de ceros, se indica que no cumplen con las condiciones de independencia lineal ni de generadoras.
- ✍️ Al documentar el proceso, se deben copiar y enumerar cada uno de los resultados de las reducciones, señalando claramente la independencia lineal y la capacidad de generación en cada caso.
- 📑 El resultado final implica describir claramente las características de cada matriz y los pasos utilizados para identificar si constituyen bases, vectores generadores o conjuntos linealmente independientes.
Q & A
¿Qué es lo primero que se debe hacer antes de comenzar el ejercicio?
-Antes de comenzar el ejercicio, se debe abrir Jupyter y otra ventana para ejecutar comandos, tal como se ha hecho en ejercicios anteriores.
¿Cuál es el objetivo del ejercicio mencionado en el guion?
-El objetivo es analizar una serie de matrices para determinar si sus columnas son linealmente independientes, generadoras o bases del espacio kn.
¿Qué es 'sage code' y cómo se utiliza en este ejercicio?
-'Sage code' es un bloque de código que contiene las definiciones de las matrices. Este bloque permite no tener que teclear manualmente todos los valores y se utiliza para facilitar el proceso de cálculo.
¿Qué se hace en cada caso con las matrices proporcionadas?
-Se reduce cada matriz para analizar si los vectores son linealmente independientes, generadores o bases, y luego se discuten los resultados caso por caso.
¿Cómo se identifican los vectores linealmente independientes en una matriz?
-Los vectores son linealmente independientes si todas las columnas de la matriz son pivote. Además, si no hay filas de ceros, los vectores también son generadores.
¿Qué ocurre si una matriz tiene una fila de ceros?
-Si una matriz tiene una fila de ceros, no es generadora. Además, si no todas las columnas son pivotes, tampoco será linealmente independiente.
¿Cómo se determina una base para un conjunto de vectores que no son linealmente independientes?
-Si los vectores no son linealmente independientes, se puede extraer una base seleccionando las columnas que sí lo sean en la matriz original, no en la reducida.
¿Qué se hace cuando los vectores son linealmente independientes pero no generadores?
-Cuando los vectores son linealmente independientes pero no generadores, se amplían a una base utilizando vectores adicionales de la matriz identidad.
¿Qué importancia tiene la matriz original en el análisis?
-La matriz original es crucial para determinar los vectores que forman una base, ya que las columnas se toman de la matriz inicial y no de la reducida.
¿Cómo se identifica un conjunto de vectores que no son ni linealmente independientes ni generadores?
-Si no todas las columnas son pivotes y hay una fila de ceros, el conjunto de vectores no será ni linealmente independiente ni generador.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
AMD T13 - Conjuntos linealmente independientes y generadores

BASE de un ESPACIO VECTORIAL Ejercicios RESUELTOS Álgebra Lineal

Autovalores y Autovectores: Diagonalización.

SUBESPACIOS Vectoriales | 2 Ejercicios RESUELTOS

Propiedades de las relaciones analizando su matriz (parte 4)

🤔 Cómo determinar si una SERIE es CONVERGENTE o DIVERGENTE | Juliana la Profe
5.0 / 5 (0 votes)
