Tamaño de Muestra para Variables Cuantitativas con Población Finita
Summary
TLDREl video proporciona una guía detallada sobre cómo calcular el tamaño de una muestra en un estudio estadístico. Se destaca la importancia de considerar tanto el tamaño de la muestra como la población para evitar resultados no concluyentes o la exposición innecesaria de sujetos a riesgos. Se aborda la diferencia entre muestras de población finita y infinita, y se ofrecen las fórmulas estadísticas para el cálculo en ambos casos. Se utiliza un ejemplo práctico con una población conocida de 1800 sujetos, un nivel de confianza del 95%, una desviación estándar de 0.5 y un error de estimación del 5% para ilustrar el proceso. El resultado muestra que se requiere una muestra de 317 sujetos, ajustada a un 10% de pérdida, totalizando en 352 sujetos para obtener una muestra representativa para la población finita. El video promete explorar en el próximo episodio cómo se calcula el tamaño de la muestra para una población infinita.
Takeaways
- 📊 La importancia de la muestra representa la información que ofrecen para realizar inferencias sobre una población.
- ⚖️ Un tamaño de muestra demasiado pequeño puede generar resultados no concluyentes, mientras que uno demasiado grande desperdiciaría recursos.
- 🧮 Se deben utilizar fórmulas estadísticas para calcular el tamaño de la muestra adecuado.
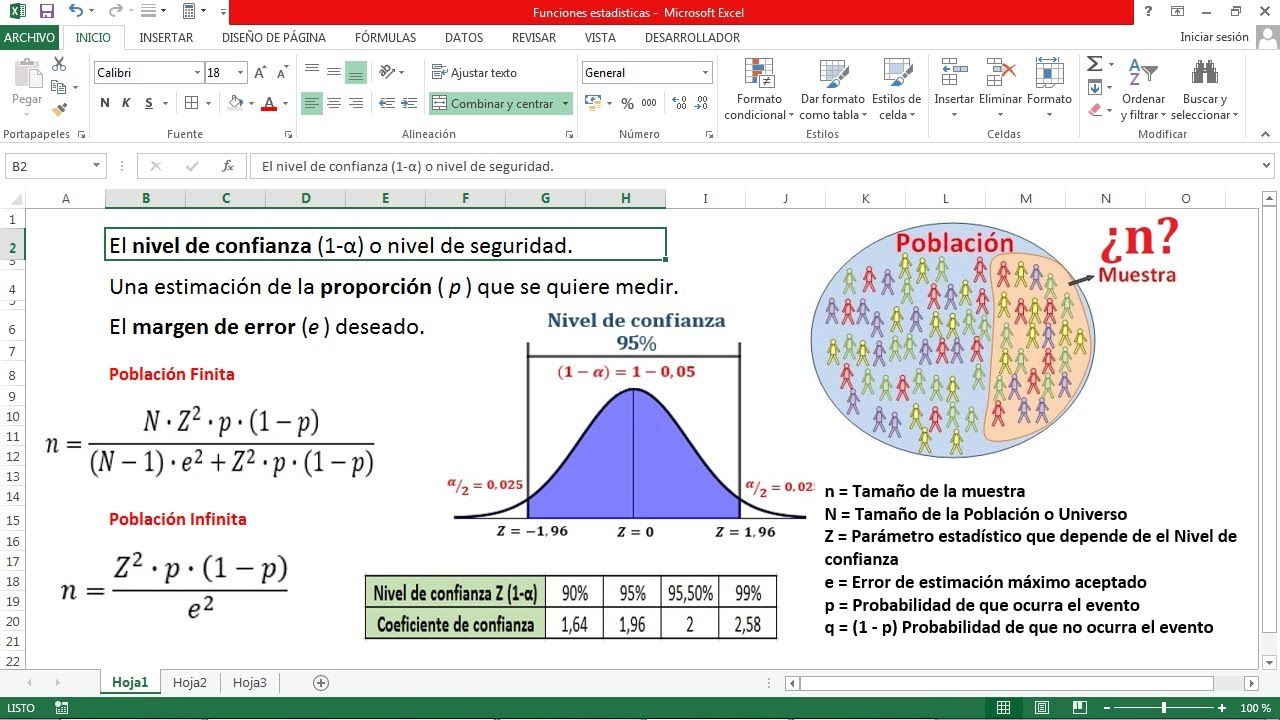
- 📈 Existen dos situaciones para el cálculo: población finita o conocida, y población infinita o indefinida.
- 📉 La fórmula para el cálculo varía según el tamaño de la población y se ajusta según el nivel de confianza y la varianza.
- 📉 El nivel de confianza comúnmente utilizado es del 95% o 99%, con valores z correspondientes de 1.96 y 2.576 respectivamente.
- 🔍 La desviación estándar es crucial ya que representa la dispersión de los datos, y es utilizada para calcular la varianza.
- 📏 El error de estimación, o precisión, es el grado de error aceptable en el estudio y generalmente se establece en un 5%.
- 🔢 La fórmula para el cálculo del tamaño de muestra para datos finitos involucra la población, el nivel de confianza, la varianza y el error de estimación.
- ➕ Se puede agregar un porcentaje de pérdida al tamaño de la muestra, usualmente no superior al 10%.
- 📚 El tamaño de la muestra ajustada por pérdidas se calcula dividiendo el tamaño de la muestra entre (1 - porcentaje de pérdida).
- 🔄 En el siguiente vídeo se explicará cómo calcular el tamaño de la muestra para una población infinita.
Q & A
¿Por qué es importante considerar el tamaño de la muestra en una investigación estadística?
-Es importante porque un tamaño de muestra demasiado pequeño puede producir resultados no concluyentes y ser poco ético al exponer a sujetos a riesgos innecesarios, mientras que un tamaño demasiado grande desperdiciaría recursos y podría exponer a más participantes de los necesarios a riesgos relacionados.
¿Cuál es la diferencia entre una población finita y una población infinita en el contexto de la selección de muestras?
-La diferencia radica en el tamaño de la población. En una población finita o conocida, se conoce el número total de individuos, mientras que en una población infinita o indefinida, el número de individuos es desconocido o muy grande.
¿Qué nivel de confianza se utiliza generalmente para calcular la muestra en una investigación estadística?
-Normalmente se utilizan niveles de confianza del 95% o 99%. Para el 95%, el valor Z es 1.96, y para el 99%, es 2.576.
¿Cómo se define la desviación estándar en el contexto de una muestra?
-La desviación estándar representa la dispersión de los datos que se han obtenido en la muestra y es un indicador de la variabilidad dentro de los datos.
¿Qué es la varianza en un estudio estadístico y cómo se calcula?
-La varianza es el cuadrado de la desviación estándar y representa la dispersión de los datos alrededor de la media. Se calcula multiplicando la desviación estándar por sí misma.
¿Qué es el error de estimación y cómo se relaciona con el tamaño de la muestra?
-El error de estimación es el grado de error de aceptación en el estudio. Es un factor crítico al calcular el tamaño de la muestra, ya que un error máximo del 5% es comúnmente utilizado para efectos prácticos e investigativos.
¿Cómo se calcula el tamaño de la muestra para una población finita?
-Para una población finita, se utiliza la fórmula n = (Z^2 * s^2 * (N-1)) / (E^2 * (N-1) + Z^2 * s^2), donde n es el tamaño de la muestra, Z es el valor de la desviación estándar del nivel de confianza, s es la desviación estándar, N es el tamaño de la población y E es el error de estimación.
¿Por qué se añade un porcentaje de pérdida al tamaño de la muestra?
-Se añade un porcentaje de pérdida para considerar posibles casos en los que los participantes no respondan o se retiren del estudio, asegurando que el tamaño de la muestra final sea representativo y estadísticamente significativo.
¿Cuál es el tamaño de la muestra ajustada a la pérdida para una población de 1800 con un porcentaje de pérdida del 10%?
-El tamaño de la muestra ajustada a la pérdida se calcula como n / (1 - porcentaje de pérdida). En este caso, sería 317 / (1 - 0.10), lo que resulta en aproximadamente 352 sujetos.
¿Cómo se relaciona el tamaño de la muestra con la precisión del estudio?
-El tamaño de la muestra直接影响研究的精确度。Un tamaño de muestra más grande generalmente proporciona resultados más precisos, pero también requiere más recursos. Un tamaño de muestra más pequeño puede ser menos preciso y más vulnerable a errores.
¿Qué se debe tener en cuenta al calcular el tamaño de la muestra para una población infinita?
-Para una población infinita, la fórmula para calcular el tamaño de la muestra es ligeramente diferente y no incluye la división por el tamaño de la población, ya que se asume que la población es ilimitada.
¿Por qué es esencial utilizar fórmulas estadísticas para determinar el tamaño de la muestra?
-Las fórmulas estadísticas son esenciales para asegurar que la muestra sea representativa de la población y proporcione resultados confiables y válidos. También ayudan a equilibrar los recursos y minimizar los riesgos éticos en la investigación.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
5.0 / 5 (0 votes)